A x sin 1/x cos 1/x B cos 1/x 2x sin 1/x C x sin 1/x cos 1/x D None of these
Y=sin^-1(2x/1+x^2) find dy/dx-Given, y = sin 1 ( 2x / 1 x 2) Let us find the derivative on both sides with respect to x We will proceed by using the inverse trigonometric concept Let us assume x = tan θ ⇒ θ = tan 1 x (1) On substituting the value of x in the given function, we get ⇒ y = sin 1 ( 2 tan θ / 1 tan 2 θ) ⇒ y = sin 1 ( sin 2θ) = 2θ1Find dy/dx of the following y= 2x 3 e −3x y= 5e −3x^2 y= ln2x y=1/(1−x) y= x (x1) y= ln(1−e −2x) y= sin 2 3x xy= y−2
Y=sin^-1(2x/1+x^2) find dy/dxのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  |  |
 |  |  |
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 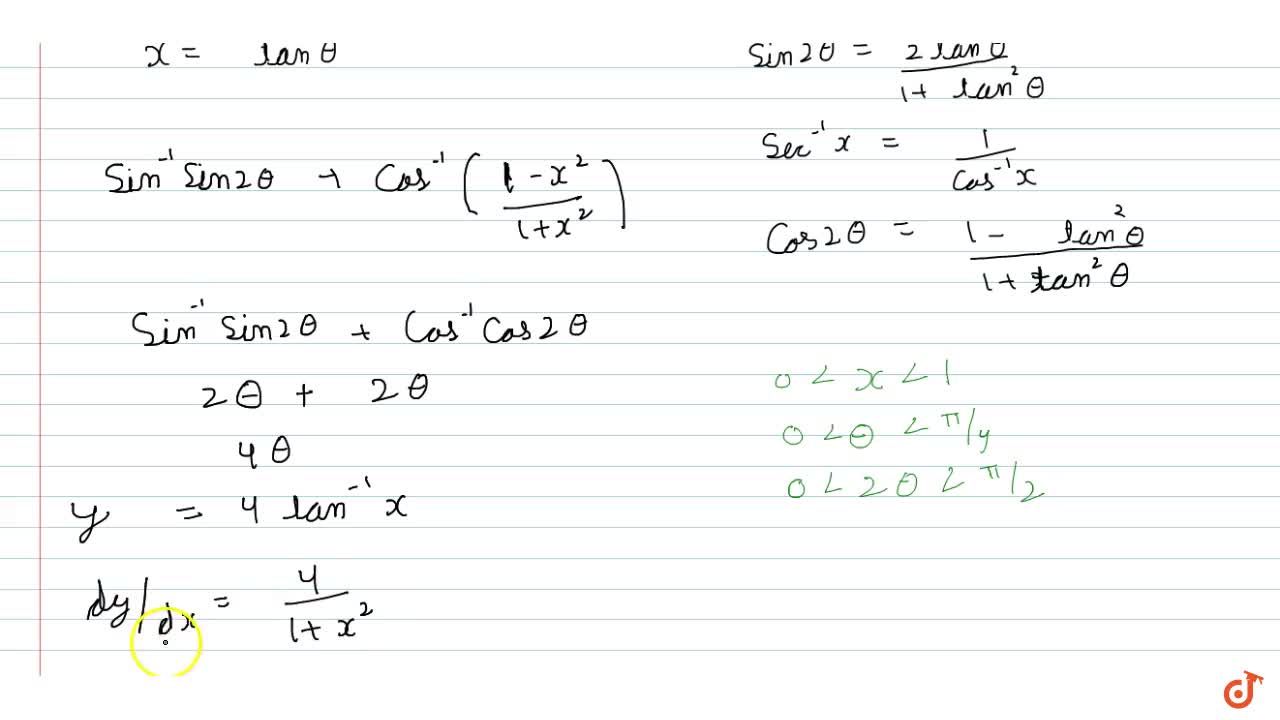 |
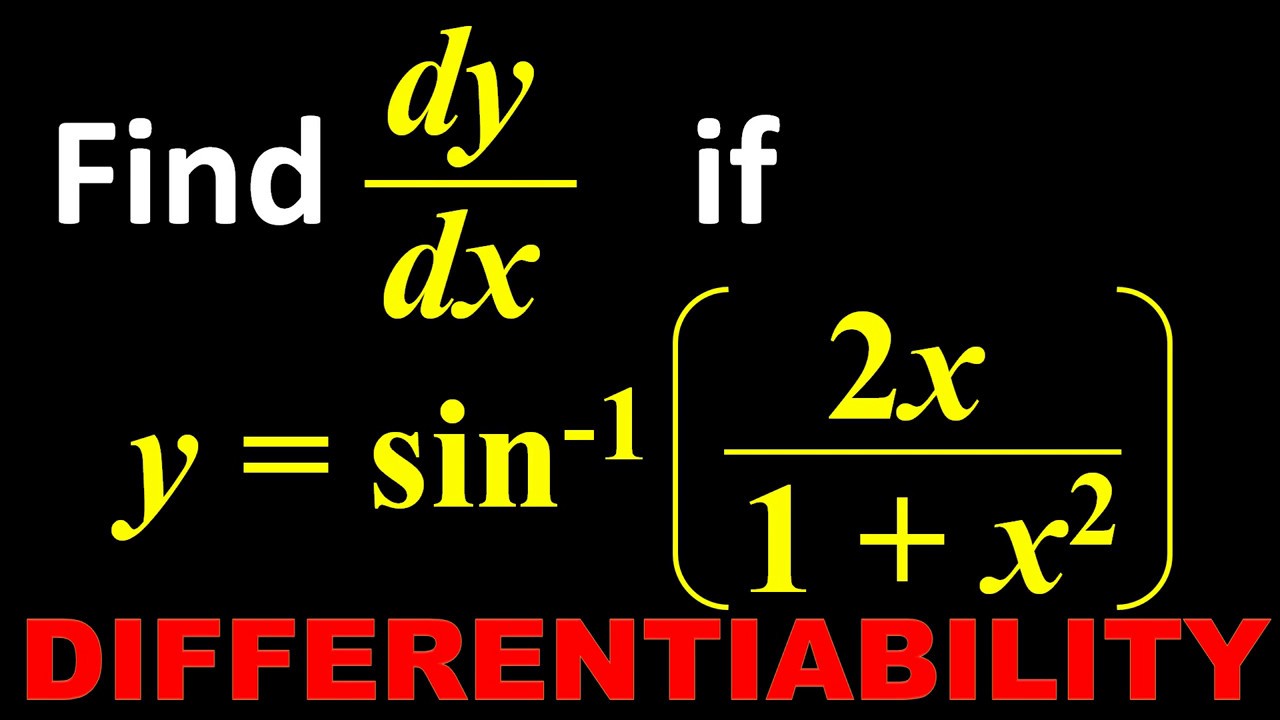 |  | |
 | ||
 |  |  |
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
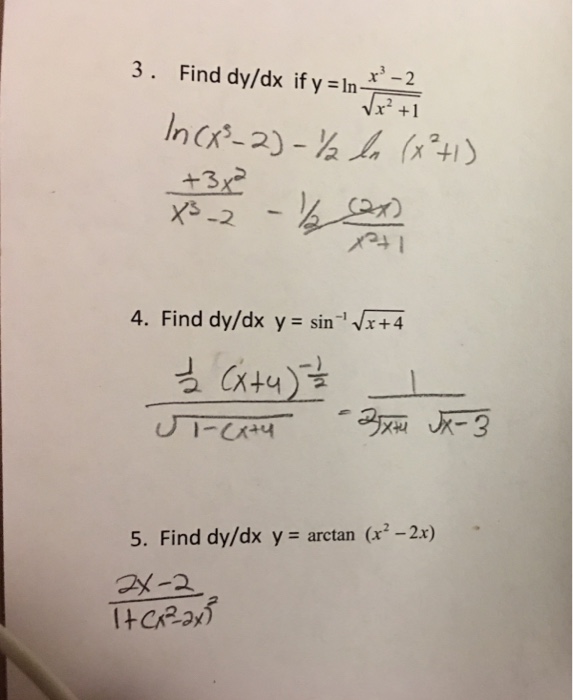 |  |  |
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
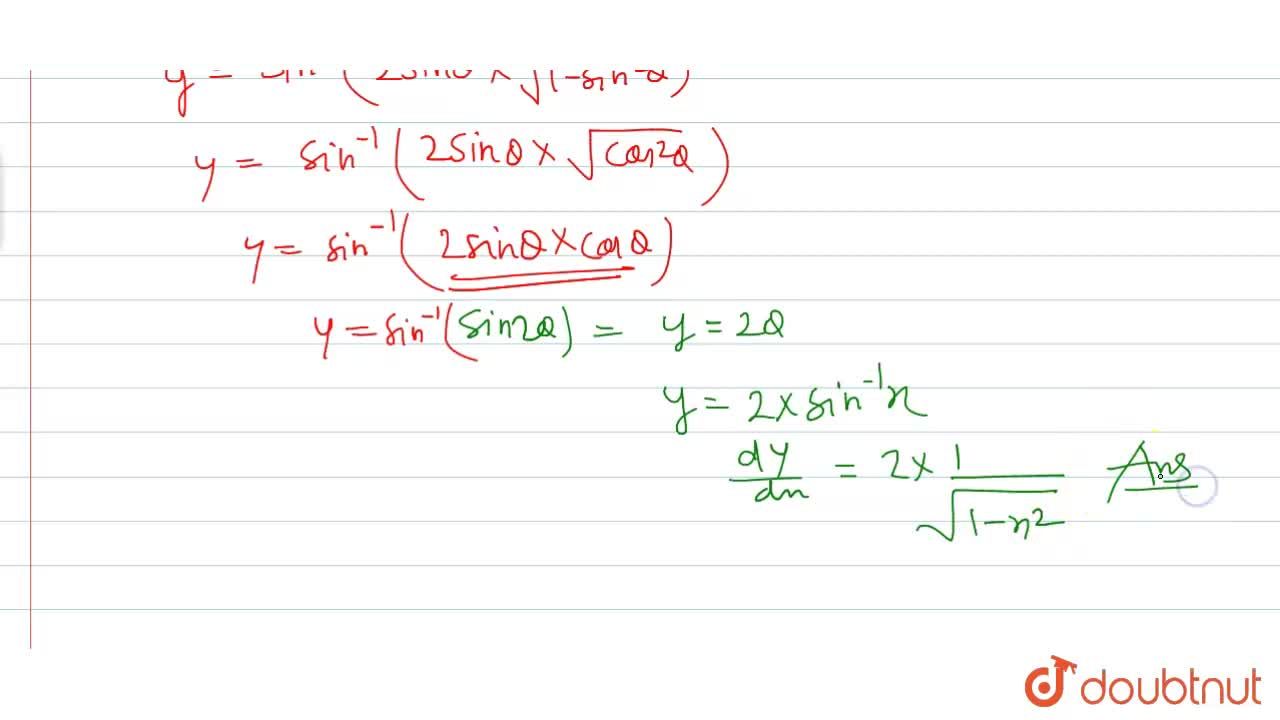 |  | |
 |  | |
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  | |
「Y=sin^-1(2x/1+x^2) find dy/dx」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |
A wave equation which gives the displacement along the ydirection is given by A wave equation which gives the displacement along the ydirection is g iven by y = 10– sin (60 t 2x) where x and y are in metres and t is time in seconds This represents a waveExample Solve this (k is a constant) dy dx = ky Step 1 Separate the variables by moving all the y terms to one side of the equation and all the x terms to the other side Multiply both sides by dx dy = ky dx Divide both sides by y dy y = k dx Step 2 Integrate both sides of the equation separately Put the integral sign in front ∫ dy y
Incoming Term: y=sin^-1(2x/1+x^2) find dy/dx,




0 件のコメント:
コメントを投稿