If A 2 B 2 C 2 And A B C 0 Find Ab Ca Sarthaks Econnect Largest Online Education Community
After trying a lot, I've got a simple solution Suppose that, $2≤a≤b≤c$ Note that, $$abbcca2Algebra Factor abbcb^2ac ab bc b2 ac a b b c b 2 a c Reorder terms b2 abbcac b 2 a b b c a c Factor out the greatest common factor from each group Tap for
Ab=bc=25 ac=14
Ab=bc=25 ac=14-We know that , (abc)^2=a^2b^2c^22ab2bc2ca we also solve this by substituting AB in place of 'a' , 'BC'in place of 'b' and 'CA' in place of 'c' in above equation More answers below Ex 91, 3 Add the following (i) ab − bc, bc − ca, ca − ab Expressions are ab − bc bc − ca ca − ab We put like terms below like terms So, required sum = 0

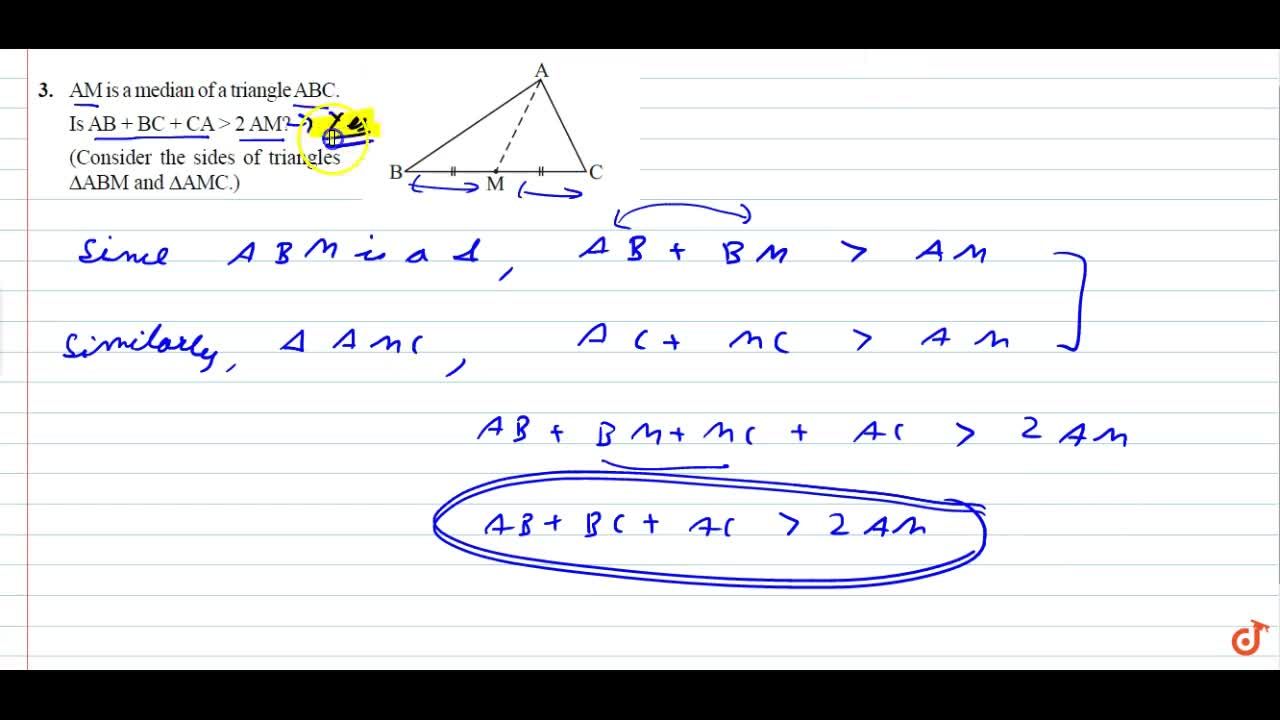
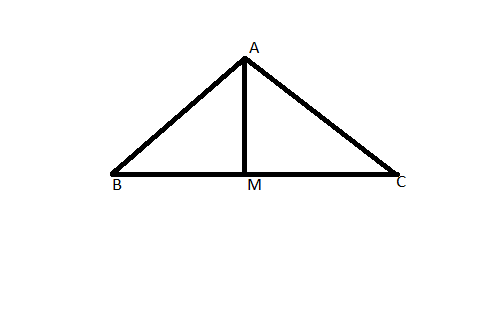
Am Is A Median Of A Triangle Abc Is Ab Ca 2 Am Consider The Sides Of Triangles Abm And Amc
If a>0, b>0, c>0 and a b > c, b c > a, c a > b then ( a b c )^2Divide each term in 2(abbc ca) = v 2 ( a b b c c a) = v by 2 2 and simplify Tap for more steps abbc ca = v 2 a b b c c a = v 2 Subtract bc b c from both sides of the equationA 2 b 2 c 2 2 (ab bc ca) = 625 a 2 b 2 c 2 2 × 59 = 625 Given, ab bc ca = 59 a 2 b 2 c 2 118 = 625 a 2 b 2 c 2 118 – 118 = 625 – 118 subtracting 118 from both the
Why some people say it's true Just like with multiplication, the order that you choose to evaluate the two division operations doesn't matter Why some people say it's false It's almost never true (i) ab bc, bc ca, ca ab (ii) a b ab, b c bc , c a ac (iii) 2 p 2 q 2 3pq 4, 5 7pq 3 p 2 q 2 (iv) l 2 m 2, m 2 n 2, n 2 l 2, 2lm 2mn 2nl Solution The givenIf a b c = 1, ab bc ca = 2 and abc = 3, then the value of a4 b4 c4 is equal to UhOh!
Ab=bc=25 ac=14のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
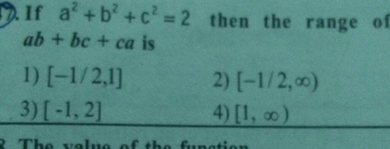 | ||
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 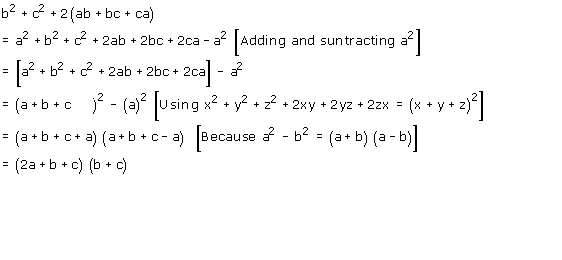 |  |
 | ||
 |  |  |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Ab=bc=25 ac=14」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
We have to prove that a=b=c Solution a² b² c² = ab bc ca (Given) On multiplying both sides of the equation with 2, we get 2 ( a² b² c² ) = 2 ( ab bc ca) 2a² 2b² 2c² = 2ab 2bcTo prove this equation nonnegative, you will have to convert the equation in terms of perfect square form containing a,b and c Now, a²b²c²abbcca = ½ • ( 2a²2b²2c²2ab2bc 2ca )
Incoming Term: (ab+bc+ca)^2, ab+bc+ca 2am, ab+bc+ca+2abc=1, (ab+bc+ca)^2 formula, ab+bc+ca 2ad, (ab+bc+ac)^2, ab+bc+2a+2c, ab=bc=20 ac=24, ab=bc=26 ac=20, ab=bc=25 ac=14,




0 件のコメント:
コメントを投稿